This is the question that every new student I have asks after a few games played. I've wondered this myself. Through my two decades of playing the game I've read a great deal on the history of the evolution of the board itself.
Today, in general, we play on boards that are 19x19, but this wasn't always so. In Ancient times Go was played on boards from 15x15, 17x17, and 19x19. Somewhere around the 200CE we see everyone settle out on the 19x19 board.
Received wisdom is the reason why is because the outside/territory is just about equal to the inside/influence using the 3rd/4th line as the demarcation between the two.
If you are more mystically minded the reasoning given were that the number of points, 361, represents the days of the year, the 4 quadrants the seasons, the stones the equal balance of yin and yang, etc., etc., etc.
I am much more mathematically, and mechanically, inclined so I needed to know more and for certain!
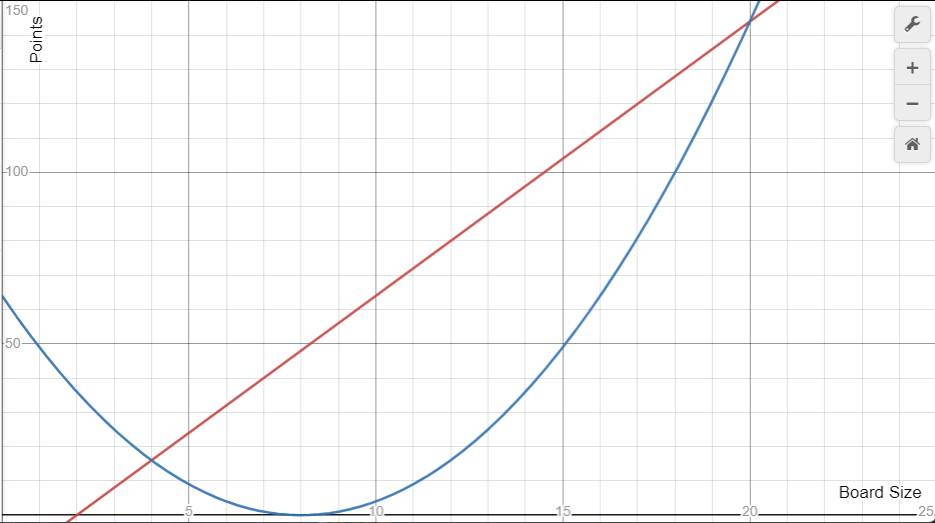
How many points are there between the two regions? If you were to place stones on the 3rd and 4th lines to split the board into two regions, inside and outside, you'd end up with a board that looks like below. 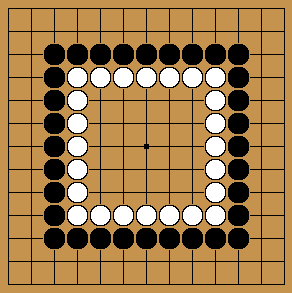
To calculate the number of points I used the following (if you want how I derived these equations see this post here)
- Total number of points: $N^2$
- Points on the outside: $8(N-2)$
- Points occupied by stones: $8(N-6)$
- Points on the inside: $N^2 - 16(N-4)$
For the 19x19 board this turns into:
- 361
- 136 (this could be 140 if you omit the corners)
- 104
- 121
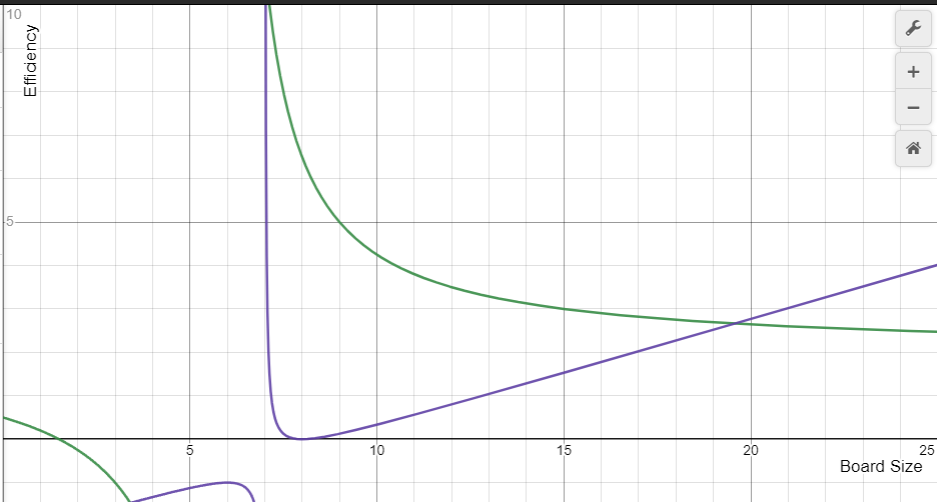
This shows that there are slightly more points on the outside than the inside. The next thought is what about efficiency? How many stones did it take to get that 136 points on the outside vs the 121 in the center?
Here's some more equations
- Outside Stones: $4(N-5)$
- Inside stones: $4(N-7)$
- Efficiency: Points/Stones Played
And the values turn out to be:
- 56
- 48
- Black: 2.428 (2.69 if you omit the corners)
- White: 2.52
If we could play go on boards where we could have $\mathbb{R}$ sized boards then the most efficient sized board would be 19.573 and the board with the perfect balance of inside and outside stones would be 20, exactly.