Derivations for "why 19x19" post

By zehaeva, 19 February, 2024

A lot of this noodling was done on paper but I've replicated it here. It's pretty basic and explicit but I find it nice to not just wave your hands and go "and here's the answers". I catch more errors myself this way. And who knows, maybe I messed it up!

Points

So first I laid out a 13x13 board so I could group the points together 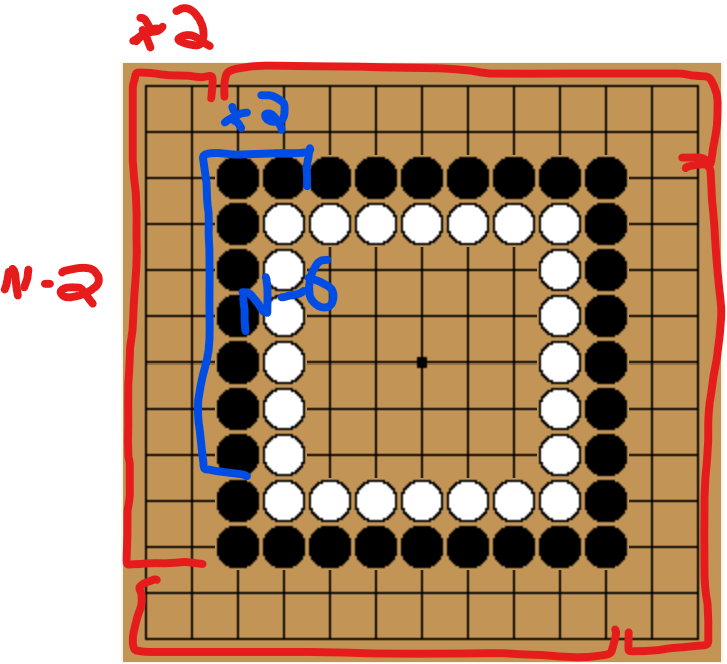For the outside I was thinking that we had 4 N by 1 groups and then 4 (N - 4) by 1 groups, but then I thought of the above groupings which gives us 8 (N-2) groups, this makes the math a bit easier to deal with, and the same logic can be applied to the stones that make up the wall.

  • Outside Points
  • $(N-2) * 2 * 4 == 8(N-2)$
  • Stones on the board
  • $(4*2 *(N-6))== 8(N-6)$

So for the inside points we just need to subtract the outside points and the stones from the total number of points.

  • Inside Points
  • $N^2 - [8(N-2) + 8(N-6)] $
  • $N^2 - [8(N-2 + N - 6)]$
  • $N^2 - [8(2N - 8)]$
  • $N^2 - [16(N - 4)]$

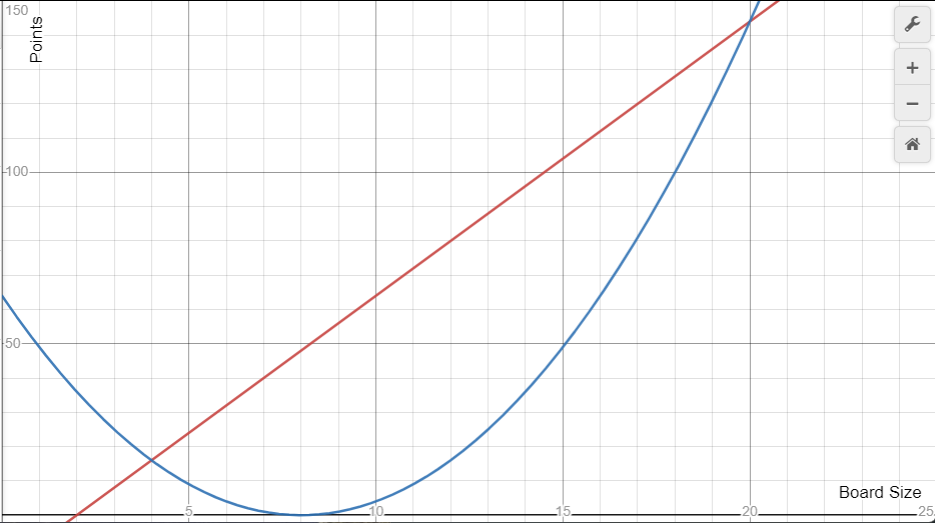
From here we have the equations for the inside and the outside points. As you can see the outside grows linearly and the inside grows quadratically. Technically we have two points where the points are balanced, as you can see from the graph, but one definitely makes more sense to go towards than the other.

a graph of the points on the inside, in red, and the points on the outside, in blue

Efficiency

So I had to redo the equations for the stones to get the efficiencies; before I was lumping all the stones together instead of separating them. To be honest I don't think this efficiency argument holds a ton of water given that the number of stones "played" are not the equal at this point in the "game". But I guess the same could be said about efficiency arguments for making life in the various places around the board.

I performed a similar grouping as I did the first time, but applied only to the stones on the inside and the outside

  • Outside Stones:
  • $4 * (N-5)$
  • Inside Stones:
  • $4 * (N-7)$

And after that we just divide the points by the stones played

  • Outside efficiency:
  • $\frac{8(N-2)]}{4(N-5)}$
  • Inside efficiency:
  • $\frac{N^2 - [16(N - 4)]}{4(N-7)}$
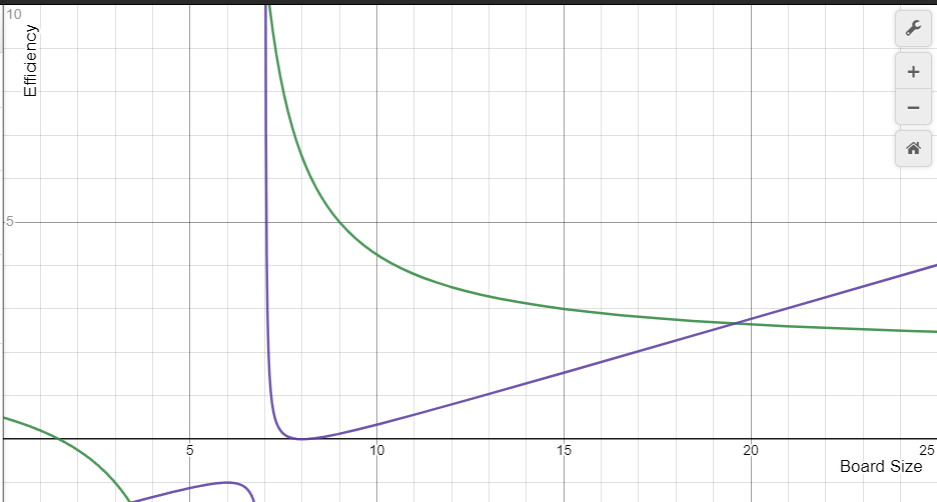
a graph of the efficiency of the inside stones, in green, and the points on the outside, in purple

The asymptote in the graph at a board size of 7 shows the inversion point/limits of where there's even an inside.

Tags